Bạn khó nhớ hoặc chưa biết cách vận dụng những công thức cấp số cộng vào giải toán thì cùng capsocong.net tìm hiểu về các công thức cấp số cộng này, cùng với những quy tắc hay ngay bây giờ. Giờ chúng ta vào chi tiết bài nhé.
1. Cấp số cộng là gì?
1.1 Định nghĩa
Theo sgk: Cấp số cộng là một dãy số (hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với một số không đỗi d.
Số d được gọi là công sai của cấp số cộng.
Nếu (un) là cấp số cộng với công sai d, ta có công thức truy hồi

1.2 Số hạng tổng quát của cấp số cộng
Khi biết số hạng đầu và công sai thì ta dễ dạng tìm được số hạng tổng quát theo công thức
un = u1 + d
- u1 là số hạng đầu
- d là công sai
- un là số hạng tổng quát

1.3 Tính chất
Tính chất: Trong một cấp số cộng, mỗi số hạng (trừ số hạng đầu và cuối) đều là trung bình cộng của hai số hạng đứng kề với nó, nghĩa là
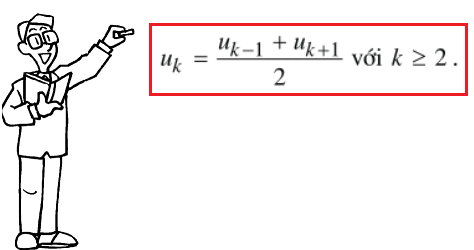
1.4 Tổng n số hạng đầu
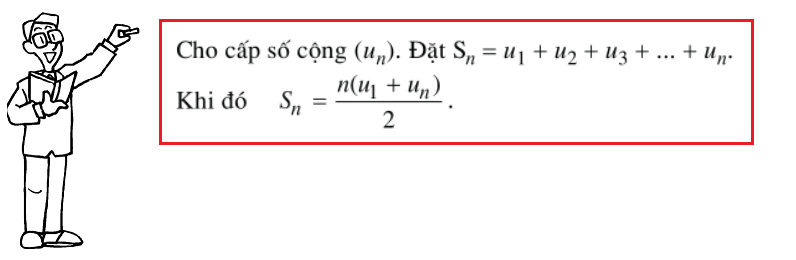
2. Các công thức cấp số cộng hay dùng
- ${u_n} = {u_{n – 1}} + d$ với n ≥ 2
- ${u_n} = {u_1} + \left( {n – 1} \right)d$
- ${u_n} = \frac{{{u_{n + 1}} + {u_{n – 1}}}}{2}$
- ${u_n} = {u_m} + \left( {n – m} \right)d$
- ${S_n} = {u_1} + {u_2} + … + {u_n} = \frac{{n\left( {{u_1} + {u_n}} \right)}}{2}$ với n ≥ 1
- ${S_n} = n{u_1} + \frac{{n\left( {n – 1} \right)}}{2}.d$ với n ≥ 2
3. Bài tập vận dụng
Bài tập 1. Xác định công sai, số hạng thứ 5, số hạng tổng quát và số hạng thứ 100 của mỗi cấp số cộng sau:
a) 4, 9,14, 19,…;
b) 1, -1, -3, -5,…
Lời giải
a) Cấp số cộng có: \({u_1} = 4,\) công sai \(d = 5\)
Số hạng tổng quát của dãy số là: \({u_n} = 4 + 5\left( {n – 1} \right) = 5n- 1\)
Số hạng thứ 5: \({u_5} = 5.5- 1 = 24\)
Số hạng thứ 100: \({u_{100}} = 5.100- 1 = 499\)
b) Cấp số cộng có: \({u_1} = 1,\) công sai \(d = – 2\)
Số hạng tổng quát của dãy số là: \({u_n} = 1 + \left( { – 2} \right)\left( {n – 1} \right) = -2n+3\)
Số hạng thứ 5: \({u_5} = (-2).5+3 = – 7\)
Số hạng thứ 100: \({u_{100}} = (-2).100+3 = – 197\)
Bài tập 2. Viết năm số hạng đầu của mỗi dãy số \(\left( {{u_n}} \right)\) sau và xét xem nó có phải là cấp số cộng không. Nếu dãy số đó là cấp số cộng, hãy tìm công sai d và viết số hạng tổng quát của nó dưới dạng \({u_n} = {u_1} + \left( {n – 1} \right)d\)
a) \({u_n} = 3 + 5n;\)
b) \({u_n} = 6n – 4\);
c) \({u_1} = 2,\;{u_n} = {u_{n – 1}} + n\);
d) \({u_1} = 2,\;{u_n} = {u_{n – 1}} + 3\).
Lời giải
a) u1 = 8; u2 = 13; u3 = 18; u4 = 23; u5 = 28.
Ta có: un – un – 1 = 3 + 5n – [3 + 5(n – 1)] = 5, ∀n ≥ 2.
Vậy dãy số \(\left( {{u_n}} \right)\) là cấp số cộng với \({u_1} = 8\) và công sai \(d = 5\).
Số hạng tổng quát: \({u_n} = 8 + 5\left( {n – 1} \right)\).
b) u1 = 2; u2 = 8; u3 = 14; u4 = 20; u5 = 26.
Ta có: un – un – 1 = 6n – 4 – [6(n – 1) – 4] = 6, ∀n ≥ 2.
Vậy dãy số \(\left( {{u_n}} \right)\) là cấp số cộng với \({u_1} = 2\) và công sai \(d = 6\).
Số hạng tổng quát: \({u_n} = 2 + 6\left( {n – 1} \right)\).
c) u1 = 2; u2 = 4; u3 = 7; u4 = 11; u5 = 16
Ta có: \({u_n} – {u_{n – 1}} = n,\;\) n biến động.
Suy ra đây không phải là cấp số cộng.
d) u1 = 2; u2 = 5; u3 = 8; u4 = 11; u5 = 14
Ta có: \({u_n} – {u_{n – 1}} = 3\).
Vậy dãy số \(\left( {{u_n}} \right)\) là cấp số cộng với \({u_1} = 2\) và công sai \(d = 3\).
Số hạng tổng quát: \({u_n} = 2 + 3\left( {n – 1} \right),\;\forall n \ge 2\).
Bài tập 3. Một cấp số cộng có số hạng thứ 5 bằng 18 và số hạng thứ 12 bằng 32. Tìm số hạng thứ 50 của cấp số cộng này.
Lời giải
Số hạng tổng quát của cấp số cộng: \({u_n} = {u_1} + \left( {n – 1} \right)d\).
Ta có:
\(\left\{ \begin{array}{l}{u_5} = {u_1} + 4d = 18\\{u_{12}} = {u_1} + 11d = 32\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{u_1} = 10\\d = 2\end{array} \right.\)
\( \Rightarrow {u_n} = 10 + 2\left( {n – 1} \right) = 2n + 8\).
Số hạng thứ 50: \({u_{50}} = 2.50 + 8 = 108\).
Bài tập 4. Một cấp số cộng cố số hạng đầu bằng 5 và công sai bằng 2. Hỏi phải lấy tổng của bao nhiêu số hạng đầu của cấp số cộng này để có tổng bằng 2700?
Lời giải
Ta có: \({S_n} = \frac{n}{2}\left[ {2 \times 5 + \left( {n – 1} \right) \times 2} \right] = 2700\;\)
\( \Leftrightarrow \frac{n}{2}\left( {8 + 2n} \right) = 2700\;\)
\( \Leftrightarrow {n^2} + 4n – 2700 = 0\;\)
\( \Leftrightarrow \left[ \begin{array}{l}n = – 54(L)\\n = 50(TM)\end{array} \right.\)
Vậy phải lấy tổng 50 số hạng đầu
Bài tập 5. Giả sử một chiếc xe ô tô lúc mới mua là 680 triệu đồng. Cứ sau mỗi năm sử dụng, giá của chiếc xe ô tô giảm 55 triệu đồng. Tính giá còn lại của chiếc xe sau 5 năm sử dụng.
Lời giải
Ta có: \({u_0} = 680,\;d = – 55 \).
Giá của chiếc xe sau 1 năm là: \({u_1} = 680 – 55 = 625\).
Giá của chiếc xe sau n năm là: \({u_n} = {u_1} + (n-1)d= 625 + \left( {n – 1} \right)\).(-55).
Vậy sau 5 năm sử dụng giá của chiếc xe là: \({u_5} = 625 – 55\left( {5 – 1} \right) = 405\) (triệu đồng).
Bài tập 6. Một kiến trúc sư thiết kế một hội trường với 15 ghế ngồi ở hàng thứ nhất, 18 ghế ngồi ở hàng thứ hai, 21 ghế ngồi ở hàng thứ ba và cứ như vậy (số ghế ở hàng sau nhiều hơn 3 ghế so với số ghế ở hàng liền trước nó). Nếu muốn hội trường đó có sức chứa ít nhất 870 ghế ngồi thì kiến trúc sư đó phải thiết kế tối thiểu bao nhiêu hàng ghế?
Lời giải
Ta có: \({u_1} = 15,\;d = 3\)
\({S_n} = \frac{n}{2}\left[ {2 \times 15 + \left( {n – 1} \right) \times 3} \right] = 870\)
\(\frac{n}{2}\left( {27 + 3n} \right) = 870\)
\(\begin{array}{l} \Leftrightarrow 3{n^2} + 27n – 1740 = 0\\ \Leftrightarrow \left[ \begin{array}{l}n = 20\\n = – 29(L)\end{array} \right.\end{array}\)
Vậy cần phải thiết kế 20 hàng ghế.
